На плечах гигантов, на спинах электронов
Кубок Полесья-2001, Гомель 2001-05-05
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Он принадлежит классу не-математиков.
Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
Если бы Клейн был математиком, то он должен был бы принадлежать хотя бы одному классу, но он не не принадлежит никакому из них, след, по закону контрапозиции математиком не является
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Число Непера
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
k=3
Вопрос 20:
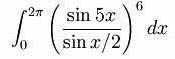
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
"счастливый"
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
Курск-2006 2006-01-07
5 тур
Вопрос 23:

На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
хайку (хокку)
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Он принадлежит классу не-математиков.
Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
Если бы Клейн был математиком, то он должен был бы принадлежать хотя бы одному классу, но он не не принадлежит никакому из них, след, по закону контрапозиции математиком не является
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Число Непера
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
k=3
Вопрос 20:
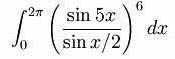
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
"счастливый"
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
Курск-2006 2006-01-07
5 тур
Вопрос 23:

На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
хайку (хокку)
-
-
18.10.2008 в 17:37это просто задача
По-видимому, красивая задача
-
-
18.10.2008 в 17:42-
-
18.10.2008 в 17:42По-видимому, красивая задача
Триумф создателей фильма.
Не просто абракадабру написали, а что-то типа формулы.
-
-
18.10.2008 в 17:44То есть в верхней формуле домен отображения может быть очень кривоват (((
Но это нам радости не прибавит.
-
-
18.10.2008 в 17:54Ну вот что вы прицепились к триумфу.
Нужны еще версии.
Не думайте о белой обезьяне
-
-
18.10.2008 в 17:55ты прочла Перес-Реверте?
Это хто вообще такой?
-
-
18.10.2008 в 17:58это автор современный.
-
-
18.10.2008 в 18:01это автор.
И его много.
Я не знаю: насколько корректно в него лезть? (((((((((
Фабий здесь?
Спросить, может?
-
-
18.10.2008 в 18:01Во, литератор Вы наш))) Не помните, чего там герой продавал в количестве больше 5 тыщ?
-
-
18.10.2008 в 18:02Но вот смотрите: если у нас есть "Тени разума" и речь в первой формуле идет о дополнении (т.е. об отрицании), и вообще, формула "осмысленная" и "красивая", как нам об этом говорят, то может это "свет разума" ???
Как считаете?
-
-
18.10.2008 в 18:03Или что в среднем бывает один из восемнадцати? У меня пока только жемчуг в голове - как бы из 18 раковин только в одной жемчуг. Но это от балды..
-
-
18.10.2008 в 18:03у меня его муж много читал. Я могу спросить. Только Фабий так и не ответил, можно ли...
-
-
18.10.2008 в 18:04Там фактор-группа или фактор-пространство V/W
-
-
18.10.2008 в 18:06Нет: R3\X — дополнение R3 до X
Но это я так.
Про фактор-группу знаю)))
-
-
18.10.2008 в 18:08Там нет формул
Там задается V как множество некоторых отображений R^3->x->R^3 (промежуточное звено не понимаю)
Задается W как множество всех тех элементов из V, которые чем-то являются
Ставится задача: найти размерность фактор(пространства?/группы?) V/W
Все.
Красивая , лаконичная задача
-
-
18.10.2008 в 18:10V как множество некоторых отображений R^3\X->R^3
Задается W как множество всех тех элементов из V, которые чем-то являются
Ставится задача: найти размерность фактор(пространства?/группы?) V/W
-
-
18.10.2008 в 18:11я его не читал, я его только в продаже видел. Не тянет))))))))
может там и правда про коллекцию листков клевера?
-
-
18.10.2008 в 18:12-
-
18.10.2008 в 18:13ну вообще 4-х лепестковый клевер встречается отнюдь не часто и есть смысл собирать его коллекцию - я такую живьем видел.
-
-
18.10.2008 в 18:17Говорю честно кто это за Перес-Реверте не знаю ( к своему стыду), но вот что можно продать?
или давайте возьмем интеграл. Хотя скорее всего это не нужно
-
-
18.10.2008 в 18:18это вроде как согласуется с фразой - один из 18
Дилетант, не может быть так, что взяв интеграл мы получим кривую как бы из 4 лепестков?Тьфу ты, он определенный. Там число
ХотяПеред вами формула, по которой можно вычислить точное количество ТАКИХ ИХ
это вроде не вяжется
-
-
18.10.2008 в 18:21-
-
18.10.2008 в 18:22-
-
18.10.2008 в 18:24Гений!
-
-
18.10.2008 в 18:25-
-
18.10.2008 в 18:25-
-
18.10.2008 в 18:25Я сама в паспорте ношу счастливые билеты. Верю, что помогает
*я просто только что поужинала барашкой
-
-
18.10.2008 в 18:26-
-
18.10.2008 в 18:26-
-
18.10.2008 в 18:26Клевер- счастливый,
билет - счастливый
Вот еще бы интеграл?
lyambda