На плечах гигантов, на спинах электронов
Кубок Полесья-2001, Гомель 2001-05-05
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Он принадлежит классу не-математиков.
Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
Если бы Клейн был математиком, то он должен был бы принадлежать хотя бы одному классу, но он не не принадлежит никакому из них, след, по закону контрапозиции математиком не является
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Число Непера
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
k=3
Вопрос 20:
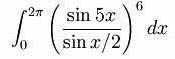
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
"счастливый"
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
Курск-2006 2006-01-07
5 тур
Вопрос 23:

На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
хайку (хокку)
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Он принадлежит классу не-математиков.
Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
Если бы Клейн был математиком, то он должен был бы принадлежать хотя бы одному классу, но он не не принадлежит никакому из них, след, по закону контрапозиции математиком не является
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Число Непера
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
k=3
Вопрос 20:
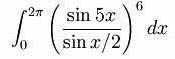
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
"счастливый"
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
Курск-2006 2006-01-07
5 тур
Вопрос 23:

На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
хайку (хокку)
-
-
18.10.2008 в 18:27Зря что ли столько задач по комбинаторике нарешали!
-
-
18.10.2008 в 18:28-
-
18.10.2008 в 18:28Бог в помощь)))
-
-
18.10.2008 в 18:28-
-
18.10.2008 в 18:29m=10^2=100
Не ((((
Если про четырезначные числа, не выходит.
Или у меня уже крыша едет.
Может, правда, счастливые...
-
-
18.10.2008 в 18:30чтоб знать общее количество, нужно знать количество цифр, которое возможно в номере. Иначе будет бесконечность (((
Как это через синусы выразить, ума не приложу (
-
-
18.10.2008 в 18:31-
-
18.10.2008 в 18:33Если он и берется то через половинный аргумент или гамма-функцию
В вопросе требуется эпитет, эпитет "счастливый"
-
-
18.10.2008 в 18:33Потом может «их» подразумевает разные существительные. Я, например, так поняла
Коллекция из.. счастливых билетов
В среднем один клевер из 18 является счастливым (я про клеверы не знаю,)
-
-
18.10.2008 в 18:35-
-
18.10.2008 в 18:36-
-
18.10.2008 в 18:36-
-
18.10.2008 в 18:37именно так=)
-
-
18.10.2008 в 18:38В продолжение темы числа. У меня 23 одно из самых несчастливых чисел, на меня в вопросе не рассчитывайте
-
-
18.10.2008 в 18:40110504*П
-
-
18.10.2008 в 18:43Как можно узнать количество счастливых если не известно количество выпущеных билетов и их табельность (количество цифр в номере)?
-
-
18.10.2008 в 18:43-
-
18.10.2008 в 18:45Ответ есть
А увязать это для себя увяжем. Вон Дилетанта опять осенит как про непрет
-
-
18.10.2008 в 18:49А что с 23?
-
-
18.10.2008 в 18:54Билеты обычно скольки значные? Отвечайте? Шести? Пяти?
А то я до ночи считать буду!
Если их в коллекции 5775, они не могут быть все разные! Иначе просто трындец! ((
-
-
18.10.2008 в 18:54-
-
18.10.2008 в 18:54про клевер ... так ляпнула.... ну если это чтото коллекционировалась как следует из задачи... может типа это были клеверы
-
-
18.10.2008 в 18:55Что может средняя часть задания касалась обычных российских билетов, то есть шестизначных
Какую коллекцию продавал герой я не знаю
-
-
18.10.2008 в 18:55А ты будешь считать все счастливые билеты стран мира? Билеты стран мира, соединяйтесь!
-
-
18.10.2008 в 18:561111
1112
1113
1114
1115
1116
1117
1118
1119
1120
1121
1122
1123
Короче, следующий после 1111 аж 1221 так? Я ничего не путаю?
Через 110 номеров ((
Это для симметричного.
А для счастливого есть еще 1120 в промежутке. Полуится в среднем 1 из 18-ти?
-
-
18.10.2008 в 18:56герой испанского автора продавал коллекцию русских билетов?
а что эта формулка изображает вообще?
-
-
18.10.2008 в 18:56Дилетант мне тоже подумалось, что это чтото связанное с разумом.... словосочетания.... а как в оригинале название фильма звучало? ум, разум, сознание? потому что это разные английские слова... скорее всего это игра слов... какаято
-
-
18.10.2008 в 18:58игры разума в оригинале Beautiful Mind
-
-
18.10.2008 в 18:59ну нет, конечно, может он как раз клеверы продавал
-
-
18.10.2008 в 19:00